Tóm tắt đề bài

SEQUENCE

Cho dãy số A[1..N]. Mỗi lần xóa ta sẽ xóa tất cả các số mang một giá trị x nào đó. Hỏi dãy dài nhất có thể tạo ra được mà không tồn tại i < j < k thỏa mãn A[i] == A[k] && A[i] != A[j]?

Giới hạn

1 <= N <= 10^5, 1 <= A[i] <= 100

AVTOGAME

Cho xâu S. Mỗi bước ta có thể chọn một đoạn l < r sao cho S[l] == S[r] và xóa đoạn đó khỏi xâu. Hỏi xâu ngắn nhất và dài nhất có thể tạo được (mà không thể xóa được tiếp) là bao nhiêu?

Giới hạn

10 test, 1 <= |S| <= 100, 'a' <= S[i] <= 'p'

DISKGAME

Cho một đĩa gồm N tầng xoay, mỗi tầng có K nấc xoay như hình dưới.

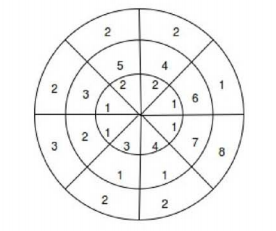
Một đĩa có 3 tầng, mỗi tầng có 8 nấc

Mỗi bước ta được xoay 1 tầng sang trái hoặc phải 1 nấc. Hỏi số bước nhỏ nhất để tạo ra 1 cột có các số bằng nhau là bao nhiêu?

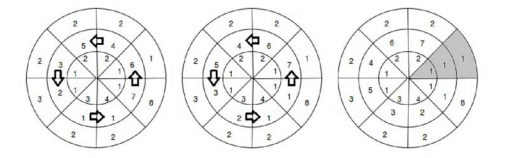
Một cách giải hình trên

Giới hạn

1 <= N, K <= 2000

Lời giải

SEQUENCE

Điều kiện của dãy số

Ta có thể thấy, 2 số x và y không được cùng tồn tại trong đáp án nếu số x bị “kẹp giữa” số y hoặc ngược lại. Ta cũng có thể dễ dàng chứng minh một dãy không tồn tại cặp x, y nào như vậy là một dãy thỏa mãn.

Ví dụ

1, 2, 1, 3, 1, 4 không thỏa mãn vì số 2 bị kẹp giữa 2 lần số 1.

Bài toán của ta trở thành đi tìm một dãy không có 2 số nào “kẹp” nhau.

Đầu và đuôi

Xét ví dụ ở trên, ta có thể thấy 2 bị kẹp giữa bởi 2 số 1 ở vị trí 1 và 3. Ta cũng có thể nói 2 bị kẹp giữa bởi 2 số 1 ở 1 và 5.

Giả sử x kẹp giữa y ở 2 vị trí a <= b, ta cũng có thể nói x kẹp ở 2 vị trí first[x] <= a và b <= last[x] (2 lần xuất hiện đầu và cuối của x). Như vậy điều kiện để x kẹp giữa y chỉ là tồn tại y nằm giữa 2 vị trí xa nhau nhất chứa x.

Đi xa hơn, ta có thể thấy xét trên trục 1 chiều, tồn tại cặp x, y kẹp nhau khi và chỉ khi 2 đoạn (first[x], last[x]) và (first[y], last[y]) giao nhau.

Quy hoạch động

Như vậy, ta chỉ cần tìm 1 tập số sao cho tập (first[x], last[x]) của các số không giao nhau. Đây là bài toán quy hoạch động cơ bản, có thể thực hiện quy hoạch động trong O(N + M) với M là số phần tử khác nhau.

Gọi f[i] là số đoạn thẳng nhiều nhất ta có thể chọn trong khoảng 1..i. Từ đây, ta có 2 lựa chọn:

Thêm khoảng không, cập nhật f[i] cho f[i + 1].
Thêm một đoạn (i + 1..j). Ta duyệt tất cả các đoạn thẳng có đầu mút trái là i + 1 và cập nhật f[i] + 1 cho f[j].

Đáp số là f[N].

AVTOGAME

Có thể xóa 1 đoạn?

Hiển nhiên các đoạn ta xóa sẽ không giao nhau, nên chỉ có 2 khả năng xảy ra để xóa đoạn [a < b]:

Nếu S[a] == S[b] ta xóa cả đoạn trong 1 bước.
Chọn 1 vị trí a < k < b - 1, xóa đoạn a..k rồi xóa đoạn k+1..b.

Dựa vào nhận xét này, ta dễ dàng dựng nên mảng canErase[l][r] (có thể xóa đoạn l..r không?) trong O(N^3):

for (int l = 1; l <= N; ++l) {
  for (int r = l + 1; r <= N; ++r) {
    if (S[l] == S[r]) canErase[l][r] = 1;
    for (int k = l + 1; k + 1 < r; ++k) {
      canErase[l][r] = canErase[l][r] || (canErase[l][k] && canErase[k + 1][r]);
    }
  }
}

Chi phí xóa hết nhỏ nhất

Thay vì giải bài toán xâu ngắn nhất còn lại, ta sẽ thay đổi bài toán bằng cách cho phép một kiểu xóa nữa: xóa 1 kí tự với chi phí 1. Sau đó ta đi tìm chi phí nhỏ nhất để xóa cả dãy. Ta có thể thấy tính chất các bước xóa rời nhau không thay đổi.

Hiển nhiên chi phí sẽ bằng đáp án, vì ta không bao giờ xóa đơn lẻ 2 kí tự giống nhau.

Để giải được bài toán này, ta cải tiến thuật toán kiểm tra tính xóa được phía trên, thành chi phí nhỏ nhất để xóa đoạn l..r. Hiển nhiên cost[i][i] = 1 vì chỉ có 1 kí tự. Với đoạn l..r ta có 2 cách xóa:

Nếu S[l] == S[r] ta xóa cả đoạn với chi phí 0.
Chọn l <= k < r rồi xóa 2 đoạn l..k và k + 1..r với tổng chi phí cost[l][k] + cost[k + 1][r].

Đáp số là cost[1][N], độ phức tạp là O(N^3).

Các kí tự còn lại

Để giải được bài toán dãy còn lại dài nhất, ta cần phải thấy tính chất của dãy còn lại. Tính chất khá đơn giản: không tồn tại 2 kí tự giống nhau trong xâu. Như vậy, ta cần nhặt ra 1 tập kí tự khác nhau sao cho các phần ở giữa có thể xóa được.

Điều kiện chỉ có 16 kí tự khác nhau cho ta một gợi ý: sử dụng bitmask để quản lí các kí tự đã lấy.

Quy hoạch động

Gọi bool f[i][mask] là tính khả thi của việc chọn ra tập kí tự thỏa mãn mask trong đoạn 1..i và xóa hết các kí tự còn lại, trong đó kí tự cuối ta chọn chính là S[i]. Ta có 2 lựa chọn:

Chọn cả kí tự S[i - 1], với điều kiện S[i - 1] != S[i] và mask có S[i - 1]. Ta lùi về trạng thái f[i - 1][mask ^ S[i]].
Chọn một vị trí j < i và lấy kí tự này là kí tự đứng ngay trước S[i]. Điều kiện là S[j] != S[i], mask có S[j] và j + 1..i - 1 xóa được. Ta lùi về trạng thái f[j][mask ^ S[i]].

Độ phức tạp sẽ là O(N^2 * 2^16), chưa thể thỏa mãn bài toán. Ta cần một chút cải tiến để xóa bớt N.

Nhảy, chọn và xóa

Ta sẽ chỉnh sửa hàm quy hoạch động một chút: xóa bỏ điều kiện S[i] là kí tự cuối cùng chọn. Thay vào đó, ta “nhảy” từng bước, chọn hoặc sử dụng duy nhất một phép xóa. Cụ thể, từ trạng thái f[i][mask], ta có:

S[i] là kí tự được chọn. Điều kiện là mask chứa S[i]. Lùi về f[i - 1][mask ^ S[i]].
S[i] là kí tự cuối cùng bị xóa. Vậy ta cần một vị trí j < i sao cho S[i] == S[j], và lùi về f[j - 1][mask].

Thoáng qua, vẫn là O(N^2 * 2^16). Làm sao để cải tiến? Ta thấy, trong trường hợp 2, điều kiện duy nhất là S[j] == S[i], mà chỉ có 16 loại kí tự, vậy ta hoàn toàn có thể lưu lại tất cả các trường hợp f[j - 1][mask] với mỗi lọai S[j] khác nhau.

Gọi g[i][mask] là tổng kết tất cả các trường hợp f[j][mask] thỏa mãn S[j + 1] == i. Ta có thể vừa đi vừa cập nhật g[S[i + 1]][mask], đồng thời trong trường hợp 2 ta chỉ cần lấy giá trị của g[S[i]][mask] trong O(1).

Độ phức tạp giảm xuống còn O(N * 2^16), thỏa mãn bài toán.

DISKGAME

Chi phí xoay của 1 đĩa

Hãy phân tích chi phí xoay của 1 đĩa để có số n ở vị trí p. Hiển nhiên chi phí là min(|x - p|) với x là các vị trí xuất hiện của n trong đĩa.

Thực chất ta chỉ cần xét đến 2 vị trí gần nhất bên trái và bên phải của p. Ta tạm gọi là x và y (để đơn giản ta coi x <= p <= y). Chi phí sẽ là min(p - x, y - p). Dễ dàng nhận thấy p - x là hàm tăng 1 đơn vị, y - p là hàm giảm 1 đơn vị với x <= p <= y. min của 2 hàm này sẽ là “núi” góc 45 độ có chóp ở trung điểm của x và y (hoặc có chóp ngang nếu trung điểm không nguyên).

Nếu ta xét tất cả các cặp vị trí liên tiếp của số, thì chi phí sẽ là nhiều “ngọn núi” như vậy.

Ta có thể thấy chi phí là một hàm như hình dưới, cho dãy 1 2 3 1 2 3 5 1 5 với n = 1. Lưu ý đoạn 8, 9, 1 cũng là 1 “ngọn núi”, vì thực chất đĩa là hình tròn.

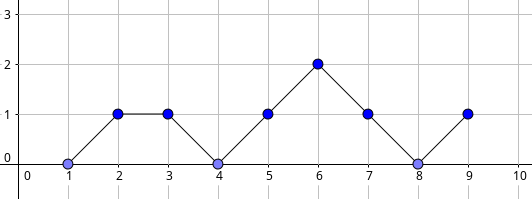
Hàm chi phí

Ta có thể cắt hàm thành các đường chéo tăng và giảm 45 độ để đơn giản hóa việc tính toán chi phí cho tất cả các đĩa.

Tổng cộng 1 đĩa sẽ bị cắt thành 2K đường chéo.

Tính tổng chi phí cho mọi đĩa

Với mỗi vị trí p và một số n, ta cần tính tổng chi phí xoay với mọi đĩa trong O(1). Biết chúng là tổng các đường chéo, làm sao để tính nhanh?

Ta sẽ vận dụng tính chất chúng đều có dạng x + b hoặc -x + b và sử dụng đường quét để tính với mỗi n.

Ta thấy, khi có k đoạn x + b[i], chi phí là kx + sum(b[i]) với bước tăng là k. Vì vậy thực chất với mỗi vị trí ta chỉ cần biết số đoạn tăng và tổng phần hằng số của chúng. Ta hoàn toàn có thể làm điều này khi quét bằng cách xét 2 đầu mút đầu (thêm đoạn) và cuối (xóa đoạn) sau đó xử lí từ trái sang phải.

Điều tương tự cũng đúng với hàm giảm.

int b[N * K + 1]; // tất cả b[i] của các đường tăng
vector<int> add[K + 2], remove[K + 2]; // các mốc thêm xóa

void addSegment(int l, int r, int id) {
  // thêm đoạn [l..r] = x + b[id]
  add[l].push_back(id);
  remove[r + 1].push_back(id);
}

void scan() {
  int value = 0, cnt = 0;
  for (int i = 1; i <= K; ++i) {
    for (auto p: add[i]) {
      value += b[p] + i - 1; // giá trị của i trước đó
      ++cnt;
    }
    for (auto p: remove[i]) {
      value -= b[p] + i - 1;
      --cnt;
    }
    value += cnt;
    // value là tổng ở vị trí i
  }
}

Ta có thể thấy độ phức tạp với mỗi n là O(K + số đoạn của n). Vì thế tổng độ phức tạp là O(K^2 + NK), do có 2NK đoạn tất cả.

Kagami Notes

2017/04/21 Training

Tóm tắt đề bài

SEQUENCE

Giới hạn

AVTOGAME

Giới hạn

DISKGAME

Giới hạn

Lời giải

SEQUENCE

Điều kiện của dãy số

Ví dụ

Đầu và đuôi

Quy hoạch động

AVTOGAME

Có thể xóa 1 đoạn?

Chi phí xóa hết nhỏ nhất

Các kí tự còn lại

Quy hoạch động

Nhảy, chọn và xóa

DISKGAME

Chi phí xoay của 1 đĩa

Tính tổng chi phí cho mọi đĩa