Lưu ý: Mình đã tóm tắt đề bài ở trên, ai không muốn bị spoil thì đừng kéo xuống lời giải vội.

Hôm nay có 5 bài của thầy Đông. Do mình không được nghe thầy chữa buổi chiều nên solution là của mình, mặc dù 99% là đúng nhưng không đảm bảo. Thực chất bài không phải là khó quá.

Tóm tắt đề bài

ACM

Có N đội, mỗi đội có 11 chỉ số A[i][1..11]. Chọn 3 đội sao cho sum[i = 1..11][max(A[x, y, z][i])] (tổng của max chỉ số từng loại của 3 đội) là lớn nhất.

Giới hạn

1 <= N <= 30000

DOMINO (Bài toán thứ nhất)

Cho một bảng M x N với K ô cấm. Điền 0 hoặc 1 vào các ô không bị cấm sao cho với ô (i, j):

Nếu i + j lẻ, thì ô (i, j) không nhỏ hơn các ô không bị cấm xung quanh.
Nếu i + j chẵn, thì (i, j) không lớn hơn các ô không bị cấm xung quanh.

Giới hạn

1 <= M, N <= 16

DOMINO (Bài toán thứ hai)

Lần này không có ô cấm. Điều kiện như bài toán thứ nhất.

Giới hạn

1 <= N <= 8, 1 <= M <= 10^6

GAMES

Cho một dãy bit N phần tử chưa xác định và M điều kiện có dạng xor của A[l..r] là 0 hay 1. Tìm vị trí x đầu tiên mà điều kiện x mâu thuẫn với các điều kiện trên.

Giới hạn

1 <= N <= 10^9, 1 <= M <= 10^5

HANOI

Cho thuật toán giải bài toán tháp Hà Nội:

def HanoiTower(height, From, Temp, To):
  if height == 1:
    # Move one from `From` to `To`
    return
  HanoiTower(height - 1, From, To, Temp)
  HanoiTower(1, From, Temp, To)
  HanoiTower(height - 1, Temp, From, To)

# Call the function
HanoiTower(N, 'A', 'B', 'C')

Tìm trạng thái của 3 tháp sau P lần gọi hàm.
Cho trạng thái của 3 tháp, tính số bước đã gọi hàm P, hoặc in -1 nếu không tồn tại trạng thái đó khi giải.

Giới hạn

1 <= N <= 100. Lưu ý P có thể là số lớn.

WG

Cho một xâu P và một tập xâu S[1..N]. Dựng xâu T như sau:

Đầu tiên chọn một xâu trong tập S[] và thêm vào T
Sau đó, tìm xâu S[i] bất kì thỏa mãn S[0] == T.back() rồi thêm S[i][1..] vào.

Hỏi xâu T ngắn nhất chứa dãy con không liên tiếp P là gì?

Giới hạn

1 <= |P| <= 250, 1 <= |S[i]| <= 10, 1 <= N <= 1000

Lời giải

ACM

Tóm tắt đề bài

Có N đội, mỗi đội có 11 chỉ số A[i][1..11]. Chọn 3 đội sao cho sum[i = 1..11][max(A[x, y, z][i])] (tổng của max chỉ số từng loại của 3 đội) là lớn nhất.

Giới hạn

1 <= N <= 30000

“Phức tạp hóa” bài toán

Rất khó để thực hiện việc chọn nếu mình sử dụng việc lấy max của từng chỉ số. Vì thế ta có thể thay đổi bài toán thành chọn 3 đội rồi mỗi chỉ số lấy của một đội. Ta có thể thấy khi có quản lí đơn giản hơn: chỉ cần mỗi đội một bitmask lựa chọn chỉ số.

Hiển nhiên khi đã xét tất cả trường hợp thì trường hợp tốt nhất luôn là lấy max.

Ghép bitmask

Giả sử ta đã chọn 3 đội i, j và k. Ta sẽ gán lần lượt 3 mask x, y, z cho 3 đội này. Các mask sẽ thỏa mãn:

Đôi một rời rạc (x & y == 0, y & z == 0, z & x == 0)
Ghép lại thì có đầy đủ (x | y | z == (1 << 11) - 1)
Tổng chỉ số tương ứng lớn nhất.

Ta có thể thấy, thực chất ta không cần quan tâm các đội được chọn là đội nào. Với mask x được chọn trước, ta chỉ cần tính xem trong các đội thì đội nào có tổng tương ứng mask x là lớn nhất. Việc 2 mask x và y bị chọn trùng đội không quan trọng: Ta có thể coi như khi đó có 1 người được chọn với mask 0.

Ta có thể tính trước max[x] với mask x trong O(N * 2^11).

Chọn 3 phần tử

Trước tiên, ta có thể thấy nếu chỉ chọn 2 phần tử, ta có thể for tất cả cặp mask, kiểm tra trong O((2^11)^2). Hiển nhiên do 2 mask đều chỉ có 11 bit nên khi or lại với nhau (ghép bộ) thì mask mới vẫn chỉ có 11 bit. Vậy để chọn 3 phần tử, ta có thể tiếp tục ghép cặp tập đã or với tập max[x].

int two[1 << 11];
int three[1 << 11];

for (int i = 0; i < (1 << 11); ++i) {
  for (int j = 0; j < (1 << 11); ++j) {
    if (!(i & j)) // không có phần tử trùng
      two[i | j] = max(two[i | j], max[i] + max[j]);
  }
}
for (int i = 0; i < (1 << 11); ++i) {
  for (int j = 0; j < (1 << 11); ++j) {
    if (!(i & j)) // không có phần tử trùng
      three[i | j] = max(three[i | j], two[i] + max[j]);
  }
}

Đáp số chính là three[(1 << 11) - 1]. Độ phức tạp sẽ là O((2 ^ 11) ^ 2).

DOMINO (Bài toán thứ nhất)

Tóm tắt đề bài

Cho một bảng M x N với K ô cấm. Điền 0 hoặc 1 vào các ô không bị cấm sao cho với ô (i, j):

Nếu i + j lẻ, thì ô (i, j) không nhỏ hơn các ô không bị cấm xung quanh.
Nếu i + j chẵn, thì (i, j) không lớn hơn các ô không bị cấm xung quanh.

Giới hạn

1 <= M, N <= 16

Quy hoạch động

Thực chất đây là một bài toán quy hoạch động bitmask cơ bản. Nhận xét rằng với mỗi ô ta chỉ cần để ý bit ô bên trái và bên trên nó để có thể xét điều kiện thỏa mãn.

Khi quy hoạch động ta đi từng ô theo từng cột, trên xuống dưới trái qua phải. Gọi f[i][j][mask] là số cách lát kể từ ô (i, j) đến cuối cùng, với mask là trạng thái N ô cuối cùng đã đến trước (i, j) (tức các ô (i - 1, j), (i - 1, j + 1), …, (i, j - 1)). Xem hính dưới:

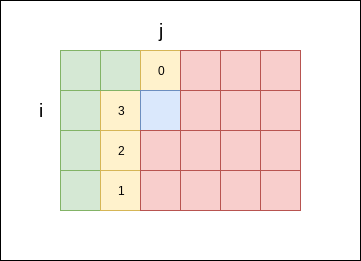
Bài Domino

Hình thể hiện trạng thái khi đã đến ô (i, j). Ô màu xanh lá là các ô đã lát, ô màu vàng thể hiện mask đang bị quản lí bởi bit tương ứng trong mask, ô màu xanh dương thể hiện ô sắp điền, ô màu đỏ thể hiện các ô chưa lát.

Để chuyển trạng thái ta xác định bit của ô (i, j), nếu nó thỏa mãn điều kiện với ô trái và trên thì gọi đến trạng thái tiếp theo (f[i][j + 1][mask mới] hoặc f[i + 1][1][mask mới] nếu đó là ô cuối của cột).

Chuyển mask như nào?

Ta để ý trên hình, bit 3, kể từ ô tiếp theo, không cần biết đến nữa. Ta có thể xóa bit này và đẩy lên, cho bit của (i, j) vào cuối. Như vậy trạng thái của mình luôn có N bit.

Độ phức tạp là O(N * M * 2^N).

Cài đặt như nào?

Nên gọi đệ quy có nhớ.

int f[20][20][1 << 16];
bool visited[20][20][1 << 16];

int cal(int i, int j, int mask) {
  if (i > M) return 1; // trường hợp biên
  if (visited[i][j][mask]) // đã tính
    return f[i][j][mask];
  visited[i][j][mask] = 1;
  for (int ch = 0; ch < 2; ++ch) {
    if (/*kiểm tra điều kiện đặt bit ch ở (i, j)*/) {
      f[i][j][mask] += cal(i + (j == N), j % N + 1, (mask << 1) & ((1 << N) - 1) + ch);
    }
  }
  return f[i][j][mask];
}

// x & ((1 << N) - 1) để lấy x % (1 << N), N bit cuối của x.
// (x << 1) == x * 2, đẩy các bit sang phải 1 đơn vị.

int ans = cal(1, 1, 0);

DOMINO (Bài toán thứ hai)

Lần này không có ô cấm. Điều kiện như bài toán thứ nhất.

Giới hạn

1 <= N <= 8, 1 <= M <= 10^6

Nhân ma trận

Lần này không có ô cấm, nên với mỗi hàng ta chỉ cần quan tâm mask của nó là gì. Từ đây ta có thể nghĩ đến việc nhân ma trận.

Giới hạn N nhỏ, M lớn cũng mang đến cho ta gợi ý này.

Số trạng thái

O((2 ^ N)^3 * log(M)) chưa thể thỏa mãn bài toán. Ta phân tích thêm một chút: với mỗi cột, ta có thể loại ra các trạng thái không thỏa mãn các điều kiện giữa 2 ô liên tiếp trên cùng cột.

Việc thử nghiệm cho thấy với N = 8 cũng chỉ có 55 trạng thái, có thể nhân ma trận.

Điều kiện theo `i + j`

Khi chuyển từ cột 2i sang cột 2i + 1, điều kiện bị thay đổi: thứ tự các ô trong cột đang từ lẻ, chẵn, lẻ, … thành chẵn, lẻ, chẵn,… Điều này làm cho việc chuyển trạng thái không thể thực hiện đơn thuần.

Ta có thể sửa điều này bằng cách thêm 1 bit cho trạng thái của cột, chỉ xem đây là trạng thái cho cột lẻ hay chẵn.

Bảng chuyển đổi của mình sẽ chỉ cho phép chuyển từ cột lẻ sang chẵn và ngược lại.

Để đơn giản từ giờ ta gọi số trạng thái là P (P <= 110).

Ma trận gốc và đáp số

Hiển nhiên ta trận gốc là một ma trận 1 x P, trong đó các ô thể hiện trạng thái cột lẻ sẽ là 1. Ta nhân ma trận gốc với bảng chuyển đổi đã lũy thừa M - 1, nhận được ma trận đáp số 1 x P. Đáp án chính là tổng các phần tử trong ma trận.

Độ phức tạp là O(P ^ 3 * log(M)).

GAMES

Tóm tắt đề bài

Giới hạn

1 <= N <= 10^9, 1 <= M <= 10^5

Chặt nhị phân

Để tìm vị trí đầu tiên mâu thuẫn, ta chặt nhị phân x để tìm vị trí xa nhất mà vẫn tồn tại một dãy thỏa mãn các điều kiện từ 1 đến x.

Bài toán trở thành kiểm tra xem có một dãy tồn tại không.

Tính chất mảng dồn

Nếu ta xét mảng dồn S[1..N], thì điều kiện tổng xor l..r bằng 0 hay 1 tương đương với S[l - 1] với S[r] bằng nhau hay khác nhau.

Ngoài ra, S[i] có thể nhận được bất kí giá trị nào không phụ thuộc vào S[i - 1] nên ta có thể thoải mái gán một giá trị bất kì, nhưng chỉ một mà thôi.

Bài toán trở thành, liệu có thể gán dãy S[1..N] thỏa mãn các điều kiện các nhau không?

2 giá trị cho 1 biến

Ta có thể coi mảng S[] như một đồ thị N đỉnh. Gộp các đỉnh cùng giá trị, ta thấy việc gán giá trị 0-1 cho các đỉnh còn lại giống như tô màu 2 phía.

Như vậy, ta có thể kiểm tra xem đồ thị có phải 2 phía không.

Độ phức tạp sẽ là O(M + N).

Giảm số lượng đỉnh

Có tận 10^9 đỉnh, tuy nhiên chỉ có 10^5 cạnh. Vì thế chỉ có tối đa 2 * 10^5 đỉnh có bậc khác 0, ta chỉ cần quan tâm tới các đỉnh này.

Độ phức tạp chỉ còn O(M), mang lại thuật toán O(M * log(M)).

HANOI

Tóm tắt đề bài

Cho thuật toán giải bài toán tháp Hà Nội:

def HanoiTower(height, From, Temp, To):
  if height == 1:
    # Move one from `From` to `To`
    return
  HanoiTower(height - 1, From, To, Temp)
  HanoiTower(1, From, Temp, To)
  HanoiTower(height - 1, Temp, From, To)

# Call the function
HanoiTower(N, 'A', 'B', 'C')

Tìm trạng thái của 3 tháp sau P lần gọi hàm.
Cho trạng thái của 3 tháp, tính số bước đã gọi hàm P, hoặc in -1 nếu không tồn tại trạng thái đó khi giải.

Giới hạn

1 <= N <= 100. Lưu ý P có thể là số lớn.

Các bước của thuật toán

Ta có thể tóm tắt thuật toán trong 3 bước:

Chuyển tháp N - 1 từ A sang B dùng C làm đệm
Chuyển đĩa N từ A sang C
Chuyển tháp N - 1 từ B sang C dùng A làm đệm

Từ thuật toán, ta có thể xác định mình đang ở bước nào bằng cách xét vị trí của đĩa N.

Nếu N còn ở A thì ta ở bước 1.
Nếu không ta ở bước 2 hoặc 3.

Sau khi xác định được vị trí của N, ta có thể bỏ nó đi và đệ quy xuống bước dưới, coi như ta đang giải bài toán chuyển tháp N - 1.

Tìm trạng thái từ `P`

Ta biết để chuyển tháp x sẽ mất 2^x - 1 bước, nên khi xét vị trí đĩa N ta có thể xác định xem ta đang ở bước mấy của việc chuyển tháp N:

Nếu P < 2^x thì ta đang ở bước 1.
Nếu P = 2^x thì ta đang ở bước 2.
Nếu P > 2^x thì ta đang ở lượt P - 2^x của bước 3.

Tùy theo bước ta xác định vị trí của đĩa N rồi đệ quy xuống bước tương ứng. Độ phức tạp là O(N). Code khá giống bò trên BST.

Tìm `P` từ trạng thái

Việc tìm P không khác gì tìm trạng thái. Khi xét tháp N, ta kiểm tra xem mình ở bước nào tùy theo vị trí của đĩa N:

Nếu N ở A, thì ta ở bước 1. Đệ quy vào bước 1.
Nếu N ở C, ta ở bước 2 hoặc 3. Cộng P thêm 2^x (cho bước 1+2) rồi đệ quy vào 3.

Độ phức tạp cũng là O(N).

WG

Tóm tắt đề bài

Cho một xâu P và một tập xâu S[1..N]. Dựng xâu T như sau:

Đầu tiên chọn một xâu trong tập S[] và thêm vào T
Sau đó, tìm xâu S[i] bất kì thỏa mãn S[0] == T.back() rồi thêm S[i][1..] vào.

Hỏi xâu T ngắn nhất chứa dãy con không liên tiếp P là gì?

Giới hạn

1 <= |P| <= 250, 1 <= |S[i]| <= 10, 1 <= N <= 1000

Tham lam dựng xâu

Khi đã có xâu T có thể lấy ra được dãy con là prefix x của P, ta có thể xác định số lượng kí tự ghép thêm khi thêm xâu S[i] bằng cách đi từ trái sang phải, tham lam kí tự tiếp theo cần ghép.

Từ đó ta tính trước được mảng nx[i][j], khi thêm xâu i với j kí tự đã ghép thì trạng thái mới là bao nhiêu. Độ phức tạp sẽ là O(N * |P| * |S[i]|).

Quy hoạch động

Ta có thể quy hoạch động f[i][j] là độ dài xâu T ngắn nhất sao cho xâu cuối cùng là i và đã ghép được j kí tự đầu tiên của P. Ta chọn thêm một xâu S[k] mới và chuyển trạng thái sang f[k][nx[k][j]]. Điều kiện là S[i].back() == S[k][0] và nx[k][j] != j.

Độ phức tạp sẽ là O(N^2 * |P|), chưa thỏa mãn bài toán.

Kí tự cuối

Thực chất ta không cần lưu chiều i là xâu cuối cùng, vì ta chỉ cần quan tâm đến kí tự cuối cùng của T, nên thay vào đó ta có thể chỉ lưu i là kí tự cuối cùng.

Độ phức tạp giảm xuống còn O(26 * |P| * N), thỏa mãn bài toán.

Tóm tắt đề bài

ACM

Giới hạn

DOMINO (Bài toán thứ nhất)

Giới hạn

DOMINO (Bài toán thứ hai)

Giới hạn

GAMES

Giới hạn

HANOI

Giới hạn

WG

Giới hạn

Lời giải

ACM

Tóm tắt đề bài

Giới hạn

“Phức tạp hóa” bài toán

Ghép bitmask

Chọn 3 phần tử

DOMINO (Bài toán thứ nhất)

Tóm tắt đề bài

Giới hạn

Quy hoạch động

Chuyển mask như nào?

Cài đặt như nào?

DOMINO (Bài toán thứ hai)

Giới hạn

Nhân ma trận

Số trạng thái

Điều kiện theo i + j

Ma trận gốc và đáp số

GAMES

Tóm tắt đề bài

Giới hạn

Chặt nhị phân

Tính chất mảng dồn

2 giá trị cho 1 biến

Giảm số lượng đỉnh

HANOI

Tóm tắt đề bài

Giới hạn

Các bước của thuật toán

Tìm trạng thái từ P

Tìm P từ trạng thái

WG

Tóm tắt đề bài

Giới hạn

Tham lam dựng xâu

Quy hoạch động

Kí tự cuối

Điều kiện theo `i + j`

Tìm trạng thái từ `P`

Tìm `P` từ trạng thái