HSGSO 2017 Editorial
Đây chắc là một trong những bài viết được chờ đợi nhất sau kì thi HSGSO 2017 vừa rồi. Ngoài chữa bài, mình sẽ đưa ra một số thống kê về đề và lượng người giải được!
Phần chữa bài được thực hiện bởi mình và bạn Nguyễn Đinh Quang Minh. Nếu có câu hỏi gì bạn có thể hỏi mình hoặc Minh qua facebook.
Đề bài
Các bạn có thể tải về đề bài tại đây. Trong phần comment của link cũng có chữa tóm tắt một vài bài do các bạn của dự tuyển Tổng Hợp.
Lời giải
Mục lục
Ngày 1
Ngày 2
number
- Author: thầy Phương, Phạm Cao Nguyên
- Tester: Nguyễn Hoàng Hải Minh
Các subtask nhỏ
- Subtask 1 (\(S \le 20\)) có thể dễ dàng giải bằng thuật quay lui, thử tất cả các trường hợp cắt với độ phức tạp \(O(M_1 \times M_2 … \times M_N)\).
- Subtask 2 (\(S \le 500, K \le 18\)): Do giới hạn của \(K\), đáp số là một số không quá giới hạn
long long, vì vậy ta có thể thực hiện đơn giản phép quy hoạch động. Gọi \(f[i][j]\) là số lớn nhất có thể tạo được nếu ta sử dụng các đoạn từ 1 đến \(i\) và lấy tổng cộng \(j\) chữ số. Hiển nhiên \(f[0][0] = 0\). Ta có: \[f[i][j] = \sum\limits_{k=0}^{\min(M_i, j)} f[i - 1][j - k] \times 10^k + \overline{A_{i,1}A_{i,2}…A_{i,k}}\] Đáp số chính là \(f[N][K]\). Lưu ý độ phức tạp của thuật toán này chỉ là \(O(SK)\) chứ không phải \(O(N^2K)\).
Tham lam 1 chữ số
Subtask 3 có một giới hạn khá lạ: Mỗi đoạn có độ dài đều là 1. Như vậy, việc chọn một đoạn chỉ đơn giản là lấy hoặc không. Ta có thể ra một thuật toán tham lam cho subtask này.
Ta có thể thấy, ở mỗi vị trí từ trái sang phải ta sẽ luôn ưu tiên số lớn nhất ở trước. Thật vậy, dễ dàng chứng minh điều này: Khi so sánh 2 số có cùng độ dài, ta chỉ cần tìm chữ số đầu tiên khác nhau từ trái sang và so sánh chúng.
Ý tưởng tham lam như sau. Giả sử ta đã lấy \(x\) chữ số, chữ số cuối cùng ta lấy ở vị trí \(i\). Ta có các nhận xét sau về chữ số tiếp theo cần lấy (ở vị trí \(j\)):
- Hiển nhiên ta không thể lấy tiếp ở các vị trí \(j \le i\).
- Hiển nhiên không kém, ta không thể lấy ở các vị trí \(j > N - (K - x) + 1\). Đơn giản là, nếu lấy ở các vị trí này, ta không còn đủ chữ số để dựng số có \(K\) chữ số nữa.
- Trong các vị trí còn lại, ta luôn chọn vị trí có chữ số lớn nhất. Điều này hiển nhiên đúng, vì về sau ta chọn thế nào thì cũng ra số lớn hơn số được tạo ra nếu ta không chọn chữ số lớn nhất ở bước này.
- Trong các vị trí có cùng giá trị, lấy vị trí trái nhất. Điều này đảm bảo ta có nhiều cơ hội hơn để lấy số lớn hơn ở vị trí tiếp theo.
Như vậy subtask 3 có thể giải với độ phức tạp \(O(10 \times N)\). Hãy lưu ý subtask này, vì ý tưởng tham lam là chìa khóa để giải subtask cuối!
Cải tiến quy hoạch động
2 subtask tiếp theo (4 và 5) chỉ là việc cài đặt công thức quy hoạch động của subtask 2 lên với số lớn. Dễ dàng nhận thấy ta chỉ phải cài đặt phép cộng số lớn, và đáp số không quá \(10^K\) nên độ phức tạp là \(O(SK^2)\).
Dễ dàng cài số lớn qua subtask 4, nhưng để qua subtask 5 sẽ cần thêm một chút cải tiến để lọt time limit (vd nén 9 chữ số vào một int thay vì giữ từng chữ số, cộng dồn đoạn để giảm số phép tính,…)
Subtask cuối
Để giải được subtask cuối, ta cần bỏ đi suy nghĩ quy hoạch động và quay lại với ý tưởng tham lam.
Tại sao ý tưởng của subtask 3 không thể áp dụng được ngay vào subtask cuối? Bởi vì trong mỗi đoạn, ta bắt buộc phải chọn 1 đoạn tiền tố để đặt vào đáp số. Nhiều khi, chữ số phía sau lớn nhưng đoạn chữ số phía trước không tối ưu.
Ta có thể chỉ xét chữ số tiếp theo của chuỗi đang lấy cuối cùng, hoặc đầu của các chuỗi phía sau. Đây là một nhận xét đúng. Thật vậy: Kiểu gì bạn cũng phải đặt chữ số đầu tiên của một chuỗi nếu lấy chuỗi đó. Và nếu chữ số đầu tiên có lựa chọn tốt hơn: điều đúng đắn là bỏ cả chuỗi.
Tuy nhiên, có một vấn đề khác. Khi có nhiều lựa chọn chữ số tiếp theo giống nhau, chọn chữ số trái cùng không phải lựa chọn tối ưu. Bản chất là vì lựa chọn của bạn còn làm ảnh hưởng đến tập đáp số tối ưu phía sau:
- Nếu \(M_i = 1\) với mọi \(i\), lựa chọn của bạn luôn là \((x_j, y_j)\) (giá trị, vị trí) với chữ số \(j\) (từ trái sang) và \(j\) luôn tốt hơn \(j + 1\).
- Khi điều kiện 1 không còn nữa, không phải lúc nào \(j\) cũng tốt hơn \(j + 1\). Xét trường hợp sau:
5 6và5 7(\(K = 2\)). Nếu bạn chọn số5bên trái, tiếp theo bạn chỉ được chọn giữa6và5cho chữ số tiếp theo. Trong khi đó đáp số hiển nhiên là57.
Tuy vậy, ta nhận thấy đáp án tối ưu vẫn luôn xuất phát từ chữ số lớn nhất, và đáp án vẫn là chọn số lớn nhất có thể ở mỗi bước. Vậy ta vẫn có thể đưa số 5 vào, chỉ có điều ta chưa quyết định đấy là số 5 ở vị trí nào. Hay hiểu kiểu khác, trước tiên ta chọn 5 của 5 6, nhưng do 5 7 có đầu 5 trùng với đuôi 5 của ta nên ta xóa 5 của 5 6 đi và thêm cả 5 7 vào.
Tóm tắt lại, thuật toán của ta như sau: Giả sử ta đã có \(i\) chữ số \(x_1, x_2, …, x_i\) (\(x_i\) ở dãy \(j\)), ta sẽ có tập lựa chọn cho chữ số tiếp theo (dãy \(p\) vị trí \(q\)) như sau:
- Nó phải thuộc dãy \(p \ge j\). Hiển nhiên ta không thể lấy lại một dãy trước đó.
- Sau nó phải có ít nhất \(K - i - 1\) chữ số (từ nó về cuối dãy, và tổng tất cả dãy phía sau).
- \(p = j\) và nó là chữ số đứng sau \(x_i\), hoặc
- \(p > j\), \(x_{i - k} = A[p][q - 1 - k]\) với mọi \(0 \le k < q - 1\). Khi chọn lựa chọn này, ta xóa tất cả \(x_{i - q + 2}..x_i\) và thêm vào \(A[p][1..q]\).
Dễ dàng chứng minh ở mỗi bước, ta đều lấy được chữ số lớn nhất có thể lấy được khi có prefix dựng từ bước trước đó (do vậy, nếu prefix tối ưu thì theo phép so sánh số, dãy mới là tối ưu). Do ở bước đầu (prefix rỗng), lựa chọn là tối ưu, nên theo quy nạp thuật toán tham là tối ưu.
Ta có thể cài thuật toán này trong độ phức tạp \(O(SK)\).
Một chút thống kê
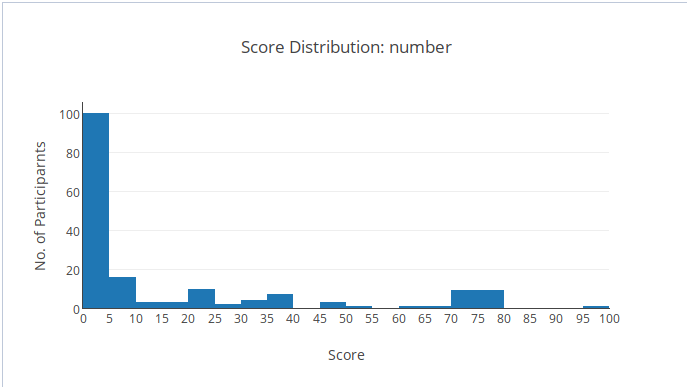
Về điểm số:
- Có một bạn duy nhất được 99 điểm (Bùi Hồng Đức). Xin chúc mừng Đức đã ra được thuật toán đúng cho subtask cuối. Thật vậy, Đức chỉ còn 1 test lắt léo duy nhất: Đề bài yêu cầu in ra số tạo từ \(K\) chữ số đã chọn, mà đã là số thì phải không có số
0ở đầu :( Kể ra bài đã khó, test cũng khó, sorry mọi người vì cái test quái gở này. - Có 12 bạn được 73-76 điểm. Khi sinh test mình đã tính đến việc các bạn sử dụng tham lam của subtask 3, đưa thẳng vào subtask 6 (chỉ qua nhận xét đầu tiên). Đây là số điểm các bạn nhận được :) Kể ra không cho điểm nào thì cũng hơi ác, nhưng cho nhiều điểm quá thì cũng không đáng (nhớ rằng tối ưu bignum chỉ được thêm 10 điểm). Thật sự 6 điểm khá là nhiều cho một thuật sai khá là rõ ràng, và còn vài bạn còn cài sai thuật đó nữa…
- 6 bạn được 70 điểm. Chúc mừng 6 bạn đã qua được mốc quan trọng của một bài khó: cắn nhiều nhất có thể. Đây là chiến thuật hữu dụng nhất khi thi quốc gia!
- Còn lại 71 bạn có điểm dương, trải dài khá đều từ 1 đến 65 điểm. Rất tuyên dương cố gắng của các bạn! Hãy cố lên! Đặc biệt với những bạn được 1 điểm, mình không hiểu tại sao có thể được 1 điểm…
Về bộ test:
- Bản thân mình khá hài lòng về bộ test mình sinh ra. Có đủ điểm cho người liều lĩnh, đủ điểm cho người chắc ăn, đủ lỗi để hành người sai,…
- Trong bộ test (sau này sẽ được up), có 2 test được sinh ra để giết một nhận xét tham lam của subtask 6… Đố bạn nào biết đó là nhận xét gì :)
race
- Author: Nguyễn Đinh Quang Minh
- Tester: Nguyễn Hoàng Hải Minh
Bài toán lớp bốn và thuật toán O(N^3)
Ba người \(A\), \(B\), \(C\) xuất phát ở ba vị trí \(x_A\), \(x_B\), \(x_C\) trên một đường thẳng, cùng đi về một hướng với vận tốc \(v_A\), \(v_B\), \(v_C\). Hỏi có thời điểm nào người \(B\) nằm ở trung điểm 2 người còn lại hay không?
Thầy Phương từng đố mình bài toán trên. Nếu bỏ qua dữ kiện ‘đây là bài toán lớp bốn’ thì chúng ta (tất nhiên kể cả mình) đều sẽ cầm bút giải phương trình bậc nhất rồi tìm nghiệm. Nhưng hãy thử nghĩ như một học sinh lớp bốn xem sao…
Cách giải của các bé lớp bốn cho bài toán này như sau: giả sử có thêm một người \(D\) di chuyển sao cho \(D\) luôn nằm ở trung điểm của \(A\) và \(C\), khi đó nếu \(B\) gặp \(D\) tức là \(B\) nằm ở trung điểm \(AC\). Vị trí xuất phát và vận tốc của \(D\) như thế nào cho hợp lý? Hiển nhiên là trung bình cộng của \(A\) và \(C\), tức là \(x_D = \dfrac{x_A + x_C}{2}\), \(v_D = \dfrac{vA + vC}{2}\).
Khi đã có người D rồi thì có 3 trường hợp xảy ra:
- \(B\) luôn chạy trùng với \(D\): có vô hạn thời điểm thỏa mãn;
- \(B\) không gặp \(D\) (kết quả tăng 0);
- \(B\) có gặp \(D\) (kết quả tăng 1).
Điều kiện cụ thể cho từng trường hợp xảy ra như sau:
| \(v_B < v_D\) | \(v_B = v_D\) | \(v_B > v_D\) | |
|---|---|---|---|
| \(x_B < x_D\) | 0 | 0 | 1 |
| \(x_B = x_D\) | 1 | vô hạn | 1 |
| \(x_B > x_D\) | 1 | 0 | 0 |
Như vậy thuật giải \(O(N^3)\) chỉ đơn giản là duyệt tất cả các bộ ba phân biệt rồi kiểm tra theo bảng trên.
Điều kiện trên nhìn quen quen?
Để tối ưu thuật toán, ta sẽ nghĩ đến việc duyệt 2 người \(A\) và \(C\), tính được thông tin người \(D\), rồi tìm số người \(B\) thỏa mãn. Cụ thể hơn:
- Nếu tồn tại người B sao cho x_B = x_D, v_B = v_D thì trả về kết quả là
infinity. - Cộng vào kết quả số người B thỏa mãn \(x_B \le X_D\), \(v_B > v_D\).
- Cộng vào kết quả số người B thỏa mãn \(x_B \ge x_D\), \(v_B < v_D\).
Hai điều kiện trên (trừ điều kiện in ra infinity rất dễ) đều khá quen thuộc: ý tưởng của nó giống với bài polylines của năm ngoái. Ta có thể sort tất cả những người \(B\) và \(D\) theo chiều \(v\) tăng dần rồi sử dụng cấu trúc dữ liệu BIT cho chiều \(x\).
Không biết cài BIT thì sao?
Thì bạn nên học cài BIT ta sẽ thử một thuật giải không sử dụng BIT mà sẽ sử dụng IT.
Trước hết, chúng ta chỉ quan tâm đến giá trị \(x\) và \(v\) của mỗi người đứng thứ mấy nên ta hoàn toàn có thể sort các giá trị \(x\) và \(v\) lại rồi “đánh số” lại theo thứ tự của giá trị trong dãy được sort. Bây giờ khi có một người \(D\) nào đó, ta có thể biết \(x_D\) đứng ở vị trí thứ mấy trong mảng \(x\) bằng chặt nhị phân, tương tự với \(v_D\). Điều này sẽ giúp ta giải quyết bài toán bằng mảng cộng dồn 2 chiều thay vì BIT.
Trước hết, ta lập một mảng \(A[1..N][1..N]\), \(A[i][j] = 1\) có nghĩa là tồn tại một người có giá trị \(x\) đứng thứ \(i\) và giá trị \(v\) đứng thứ \(j\), ngược lại \(A[i][j] = 0\). Giả sử xét một người \(D\) có \(x_D\) đứng ở vị trí thứ \(X\), \(v_D\) đứng ở vị trí thứ \(V\). Như vậy, số người thỏa mãn \(x_B \le x_D\), \(v_B > v_D\) chính là tổng các số trong hình chữ nhật con có góc trên trái là \((1, V)\), góc dưới phải là \((X, N)\) và được tính trong \(O(1)\) bằng mảng cộng dồn.
One more thing
Để cài đặt cho tiện, bạn nên nhân đôi tất cả tọa độ và vận tốc lên ¯\_(ツ)_/¯
Score Distribution!
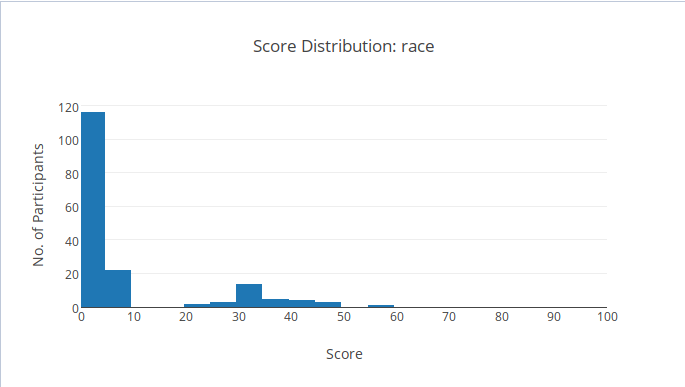
tree
- Author: Phạm Đức Thắng
- Tester: Nguyễn Hoàng Hải Minh
\(N = 1\)!
Trước tiên, cần phải để ý nếu \(N = 1\) thì đỉnh duy nhất phải có bậc 0. Khi đó, đường đi dài nhất là 1.
Rất nhiều bạn đã chết test này!
Subtask nhỏ
- Subtask 1 (\(N \le 15\)), bạn có thể backtrack mọi cách dựng cây?
Dựng được cây không?
Điều kiện sau là điều kiện cần và đủ để tồn tại cây:
- Tổng bậc là \(2N - 2\)
- Không đỉnh nào có bậc quá \(N - 1\).
- Không đỉnh nào có bậc dưới \(1\).
Dễ dàng chứng minh điều kiện này bằng quy nạp.
Subtask 2 sinh ra để bạn kiểm tra việc dựng cây nếu không biết điều này :D
Dựng tối ưu!
Gọi \(x\) là số nút có bậc lớn hơn 1 (tức không phải lá). Ta sẽ chứng minh nếu \(N \ge 2\) thì đáp số là \(x + 1\).
Thật vậy, ta gọi tập đỉnh không phải lá là \(A_1, A_2, …, A_x\). Trước tiên, dựng tập cạnh như sau:
lá - A[1] - A[2] - ... - A[x] - lá
Dễ dàng nhận thấy tổng bậc còn lại của các đỉnh không phải lá là \((2N - 2) - (N - x) - 2x = N - x - 2\), số lá còn lại là \(N - x - 2\). Như vậy ta có thể thêm lá vào các bậc còn thiếu của từng đỉnh. Cây đã dựng xong! Đường đi dài nhất trên cây này chắc chắn là \(x + 1\).
Không khó để chứng minh đáp số không thể lớn hơn \(x + 1\) (đường đi đơn không thể đi qua 3 lá). Vì vậy \(x + 1\) là đáp án tối ưu.
Phân bố điểm
Rất nhiều bạn AC bài này, tuy nhiên cũng rất nhiều người bị 98 điểm do thiếu \(N = 1\). Hãy cẩn thận với những trường hợp biên!
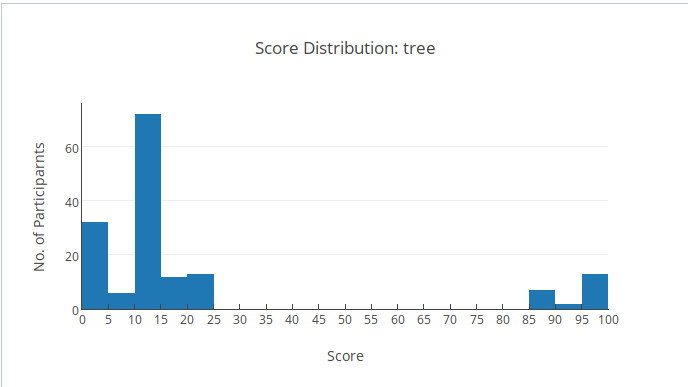
inversion
- Author: Nguyễn Thành Vinh
- Tester: Nguyễn Hoàng Hải Minh
Chạy trâu!
For từng đoạn con, tính cặp nghịch thế trâu, \(O(N^4)\) ăn sub 1. Ta có thể cải tiến hơn, tính nghịch thể trong \(O(N \log N)\) bằng BIT, tuy nhiên vẫn chưa đủ để ăn subtask 2.
Tịnh tiến Level 1
Nhận thấy, mỗi lần for đoạn con là một lần tính lại. Đoạn \((i, j)\) chỉ khác đoạn \((i, j + 1)\) một lượng là số phần tử trong khoảng \((i, j)\) mà lớn hơn \(A[j + 1]\). Như vậy, ta có thể for \(i\) rồi vừa tăng \(j\) vừa tính thêm, giảm độ phức tạp xuống \(O(N^2 \log N)\).
Tịnh tiến Level 2
Từ việc tịnh tiến trên, ta nhận thấy rằng nếu \(i \le j < k\) thì \((i, j)\) luôn có số nghịch thế không quá số nghịch thế của \((i, k)\).
Đồng thời, nhận xét cũng đúng với \((j, i)\) và \((k, i)\) nếu \(k < j \le i\).
Giả sử \(j\) là số lớn nhất sao cho \((i, j)\) có số nghịch thế \(< K\). Dễ dàng nhận thấy tất cả \((i, j’)\) với \(j < j’ \le N\) đều là đáp án. Như vậy với mỗi \(i\) ta chỉ cần tìm \(j\) là đủ.
Lại có \((i, j)\) có số nghịch thế \(< K\), vì thế \((i + 1, j)\) chắc chắn có số nghịch thế \(< K\). Ta không cần for các giá trị nhỏ hơn \(j\) để kiểm tra nữa. Thay vì for lại \(j\), ta xóa \(i\) khỏi đoạn, giảm số nghịch thế đi 1 lượng là số số nhỏ hơn \(A[i]\).
2 con trỏ \(i\) và \(j\) đều tăng từ 1 đến \(N\), mỗi lần tăng con trỏ phải update mất \(O(\log N)\). Độ phức tạp của thuật toán là \(O(N \log N)\).
Phân bố điểm
Đây là một bài khá cơ bản, dù vậy điểm khá là thấp so với bọn mình kì vọng, chủ yếu mọi người chỉ dừng ở subtask 2.
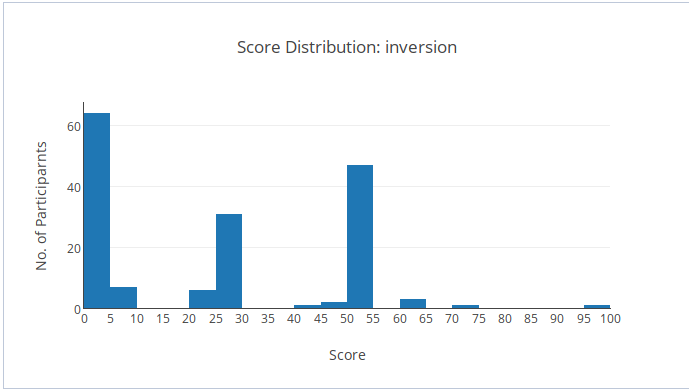
matrix
- Author: Nguyễn Đinh Quang Minh
- Tester: Phạm Cao Nguyên, Nguyễn Hoàng Hải Minh
Các subtask nhỏ
- Subtask 1 (\(N = 1\)), đây là subtask cho điểm vì bản thân cả bảng đã được chứa trong mảng \(B[]\). Nếu xor tất cả phần tử trong mảng \(B[]\) bằng \(A[1]\) thì có 1 đáp án chính là mảng \(B[]\). Nếu không thì không có đáp án nào cả. Độ phức tạp \(O(M)\).
- Subtask 2 (\(NM \le 20\)), từ điều kiện ta suy ra \(\min(N, M) \le \sqrt{20} \le 5\). Không mất tính tổng quát ta giả sử \(M \le 5\) (nếu không ta xoay bảng lại), ta có thể quy hoạch động \(f[i][mask]\) là số cách tạo các hàng từ 1 đến \(i\), với tổng xor từng cột được biểu diễn trong \(mask\). Sau đó ta có thể for tất cả các mask \(m\) có thể của hàng \(i + 1\), update vào \(f[i + 1][mask \oplus m]\). Độ phức tạp là \(O(N \times (2^M)^2)\). Hoặc ta có thể backtrack giá trị của tất cả phần tử của bảng, độ phức tạp là \(O(2^{N + M})\).
- Subtask 3 (\(N \le 10\), \(M \le 2000\)), ta sẽ cải tiến thuật toán quy hoạch động phía trên. Thay vì mỗi lần ta thêm cả cột (mất \(O(2^N)\)), ta chỉ thêm từng ô. Gọi \(f[i][j][mask]\) là số cách điền các ô từ \((i, j)\) trở đi (theo từng cột, rồi từng hàng), và xor các phần tử đã đặt vào trước đó của mỗi hàng được biểu diễn trong mask. Ta tính từ \(f[i + 1][j][mask’]\) hoặc \(f[1][j + 1][mask’]\), với điều kiện là khi điền xong mỗi cột thì xor cột đó phải bằng \(B[j]\). Ta có thể kiểm tra điều này bằng cách kiểm tra \(X = B[1] \oplus B[2] \oplus … \oplus B[j]\) có bằng xor các bit trong \(mask\) không. Độ phức tạp là \(O(NM2^N)\).
Dựng một đáp án
Trước khi tìm hiểu xem có bao nhiêu đáp án thỏa mãn, ta cần phải kiểm tra xem có tồn tại đáp án không đã.
Hiển nhiên nếu tổng xor của \(A[]\) khác tổng xor của \(B[]\) thì không thể tồn tại bảng thỏa mãn. Còn lại, ta sẽ chứng minh luôn tồn tại bảng thỏa mãn.
Gọi tổng xor cả bảng là \(S\).
Xét bảng \(N \times M\) được dựng như sau:
- Với \(i < N\) và \(j < M\): điền
0. - Với \(i = N\) và \(j < M\): điền \(B[j]\).
- Với \(i < N\) và \(j = M\): điền \(A[i]\).
- Xét ô \((N, M)\). Ta có giá trị \(b[N][M] = A[N] \oplus B[1] \oplus B[2] \oplus … \oplus B[M - 1]\), hay \(b[N][M] = A[N] \oplus S \oplus B[M]\). Tất nhiên phân tích theo cột ta cũng sẽ ra công thức này, và vì \(S\) xác định nên có duy nhất 1 cách điền ô \((N, M)\).
Vậy tồn tại bảng thỏa mãn.
Có bao nhiêu bảng thỏa mãn?
Giả sử ta có bảng \(b[][]\) thỏa mãn.
Nếu ta flip giá trị \(b[i][j]\) (\(i < N\), \(j < M\)), ta có thể flip cả \(b[i][M]\), \(b[N][j]\) và \([N][M]\) để ra một bảng mới vẫn đúng. (mỗi hàng mỗi cột ảnh hưởng đều bị flip tổng xor 2 lần).
Nếu ta giữ nguyên \(b[i][j]\) với mọi \(i < N\) và \(j < M\), dễ dàng chứng minh cách điền các ô còn lại là duy nhất. Thật vậy, \(b[i][M]\) (\(i < M\)) phải xác định duy nhất để tổng xor các ô trong hàng \(i\) bằng \(A[i]\), tương tự với \(b[N][j]\) (\(j < N\)). Còn lại ô \((N, M)\), tất nhiên vì hàng và cột cuối cũng có tổng xor xác định nên giá trị của ô cũng chỉ có tối đa một.
Từ 2 nhận xét trên, ta thấy với mỗi cách điền bảng \((N - 1)\times (M - 1)\) ở góc trái trên ta có duy nhất 1 cách điền nốt thỏa mãn. Vậy số bảng thỏa mãn là \(2^{(N - 1)(M - 1)}\).
Kiểm tra điều kiện tồn tại mất \(O(N + M)\), tính số bảng mất \(O(\log(NM))\), dựng 1 bảng thỏa mãn mất \(O(NM)\).
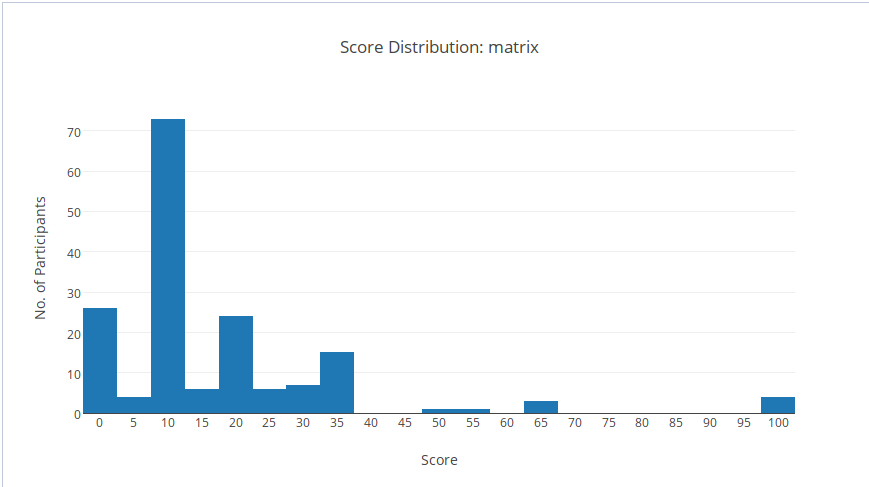
Thống kê
Subtask 2 là một subtask rất đơn giản (backtrack lấy 20 điểm), vậy mà số bạn làm được khá là ít. Subtask 3 đòi hỏi kỹ thuật quy hoạch động khó hơn, không nhiều bạn làm được.
Chúc mừng 4 bạn làm được 100 điểm!
string
- Author: Vương Hoàng Long
- Tester: Nguyễn Hoàng Hải Minh
Subtask nhỏ
Do độ dài của 2 xâu không quá \(10^8\) nên ta có thể thực hiện for trâu để giải subtask này. Tất nhiên có một số điều sau phải chú ý:
- Tuyệt đối không dựng cả xâu. Dựng xâu mất thời gian hằng số rất lớn, có thể làm bạn bị TLE trước cả khi thực hiện so sánh. Chỉ for các chỉ số lặp lại.
- Để tăng tốc, không dùng phép mod để tính nhanh chỉ số.
Độ phức tạp là \(O(|A|)\).
Subtask lớn
Để đơn giản cho việc mod ta coi xâu đánh số từ 0.
Nhận thấy phần tử thứ \(i\) của xâu \(X\) sẽ được so sánh với các phần tử \(i \mod |Y|, (i + |X|) \mod |Y|, …, (i + (n - 1)|X|) \mod |Y|\) của \(Y\).
Không khó để nhận ra dãy này có chu trình độ dài \(|Y| / \gcd(|X|, |Y|)\). Không khó để chứng minh điều này: \(|X||Y| / \gcd(|X|, |Y|)\) chính là bội chung nhỏ nhất của \(|X|\) và \(|Y|\), bội dương đầu tiên của \(|X|\) chia hết cho \(|Y|\).
Như vậy, ta chỉ cần chia \(Y\) thành các chu trình tương ứng, sau đó tính trước số kí tự từng loại là có thể so sánh 1 vị trí của \(X\) với 1 chu trình trong \(O(1)\).
Độ phức tạp là \(O(|Y| + |X|)\).
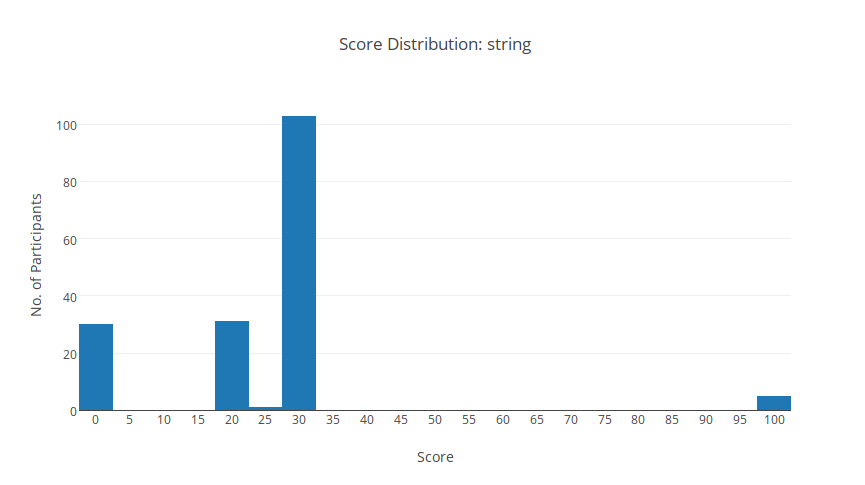
Thống kê
Đây là bài dễ của ngày 2. Tuy vậy mình không nghĩ là có ít người AC như vậy. Có lẽ tại vì không nhiều người biết đến việc chu trình BCNN?
p2grp
- Author: Nguyễn Khánh
- Tester: Nguyễn Hoàng Hải Minh
Subtask 1
Với \(n\) và \(m\) không quá 20, các cạnh không quá \(2^{m-1}\), chúng ta có thể dựng đồ thị rồi sử dụng thuật toán tìm đường đi ngắn nhất bất kì (Floyd, Dijkstra hoặc thậm chí là backtrack). Kết quả không vượt quá số nguyên 64 bit nên cũng không có gì bận tâm về cách cài đặt.
Subtask 2
Thuật toán Floyd tìm đường đi ngắn nhất cho mọi cặp đỉnh chạy trong độ phức tạp \(O(n^3)\) nên hoàn toàn có thể vượt qua subtask này. Tuy nhiên, kết quả không còn đủ nhỏ để lưu dưới dạng số nguyên nữa, vì vậy ta cần cài thêm hàm cộng 2 dãy nhị phân.
Subtask 3
Tất nhiên, ngoài Floyd, chúng ta có thể chạy thuật toán Dijkstra từ mỗi đỉnh của đồ thị. Mỗi lần chạy Dijkstra có độ phức tạp \(O((n+m) * \log n)\), nên tổng độ phức tạp sẽ là \(O(n(n+m)\log n \times C)\), trong đó \(C\) là chi phí cộng 2 dãy nhị phân.
Nếu cộng từng bit một của 2 dãy nhị phân lại với nhau thì \(C\) sẽ rơi vào khoảng 1000 phép tính, không đủ để qua subtask này. Cách tốt hơn là cứ \(x\) bit của dãy nhị phân, ta nhóm lại thành một số rồi thực hiện cộng (hiệu quả nhất là \(x = 63\)).
Subtask 4
Điều kiện \(m < n\) cho ta biết đồ thị là một cây. Giữa 2 đỉnh bất kì trên cây chỉ có duy nhất một đường đi đơn, và hiển nhiên đó là đường đi ngắn nhất.
Việc duyệt qua mỗi cặp đỉnh rồi tính đường đi ngắn nhất có vẻ không hiệu quả và cũng khó tối ưu được. Do đó chúng ta nghĩ đến việc thay đổi bài toán:
Với mỗi cạnh, có bao nhiêu cặp đỉnh mà đường đi ngắn nhất đi qua cạnh đó?
Hiển nhiên nếu ta trả lời được câu hỏi trên thì sẽ dễ dàng tính được đáp án.
Câu trả lời thực ra cũng rất đơn giản. Mỗi cạnh trên cây, nếu cắt đi sẽ tạo ra 2 cái cây nhỏ. Dễ thấy một cặp đỉnh mà mỗi đỉnh nằm ở một cây thì đường đi giữa chúng bắt buộc phải đi qua cạnh vừa bị cắt. Do vậy số cặp đỉnh có đường đi đi qua cạnh đó sẽ bằng tích độ lớn 2 cây con.
Ta đặt gốc cây ở đỉnh 1. Giả sử cạnh đang xét nối giữa đỉnh \(u\) và cha của nó, thì 1 trong 2 cây con sẽ chính là cây con gốc \(u\). Việc tính độ lớn cây con gốc u có thể giải quyết bằng DFS trong thời gian \(O(n)\).
Những cạnh không quan trọng
Đọc kĩ lại đề bài, chúng ta phát hiện ra còn một chi tiết nữa mà cả 4 subtask trước đều chưa phải dùng đến: các cạnh có độ lớn \(2^w\) và có trọng số phân biệt. Liệu đây có phải mấu chốt để giải quyết subtask cuối?
Để ý rằng trọng số của một cạnh lớn hơn hẳn tổng trọng số của các cạnh nhỏ hơn nó (vì \(2^0 + 2^1 + … + 2^{x-1} < 2^x\)). Điều đó chứng tỏ nếu 2 đường đi có cạnh lớn nhất khác nhau thì đường đi nào có cạnh lớn nhất nhỏ hơn chắc chắn có tổng nhỏ hơn.
Như vậy, ta có thể lần lượt các cạnh vào đồ thị theo thứ tự trọng số tăng dần. Giả sử khi thêm cạnh \((u, v)\) mà giữa \(u\) và \(v\) đã có đường đi thì cạnh \((u, v)\) sẽ không nằm trong bất kì đường đi ngắn nhất nào (thay vì đi cạnh \((u, v)\) ta có thể đi đường đi ngắn nhất từ \(u\) đến \(v\) đã tìm được trước đó). Do đó, ta có thể bỏ cạnh \((u, v)\).
Subtask 5 = Subtask 4 ?? :D ??
Sau khi loại bỏ các cạnh không quan trọng, đồ thị ta thu được là một cây (!). Lí do là ta sẽ không thêm cạnh \((u, v)\) mà \(u\) đã có đường đi tới \(v\), tức là đồ thị sẽ không thể có chu trình. Đến đây thì subtask 5 có thể giải y hệt subtask 4 rồi :D
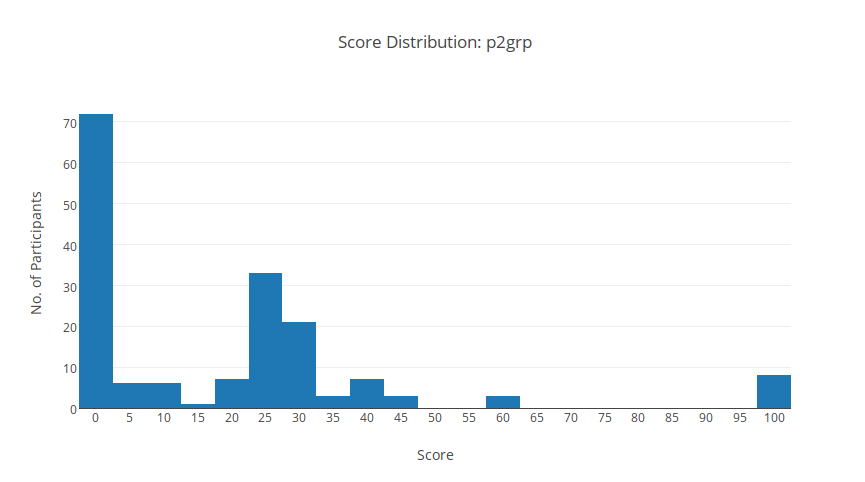
Thống kê
Đây là một bài khá lằng nhằng để ăn điểm những sub nhỏ, nhưng thuật toán chuẩn không cần quá nhiều chi tiết cài đặt. Vì thế bài có nhiều người AC, nhưng lượng ăn subtask nhỏ nhỏ hơn.
Chúc mừng 8 bạn đã AC! Fun fact: 4/8 bạn giải được bài này là của THPT Chuyên Lương Thế Vinh.
turtle
- Author: Nguyễn Đinh Quang Minh
- Tester: Nguyễn Hoàng Hải Minh
BFS trạng thái
Subtask 1 có giới hạn \(N \le 10\), nên chỉ có \(10! = 3.628.800\) trạng thái, hơn nữa từ một trạng thái có thể đi được đến tối đa là \(N-1\) trạng thái khác. Vì vậy chỉ cần BFS để tìm đường đi ngắn nhất từ trạng thái hiện tại đến trạng thái đích.
\(N \le 20\)?
Mình thành thật xin lỗi các bạn đã bỏ công để nghĩ cách lấy 60% số điểm từ subtask 2, vì thực ra mình cũng không có cách giải nào (không phải thuật chuẩn) mà qua được subtask này cả :( . Có lẽ một thuật backtrack đặt cận tốt có thể ăn được một vài test của subtask này, nhưng mình không chắc chắn lắm.
pos[a[i]] = i
Thoạt nhìn, bước biến đổi hoán vị trong bài toán có vẻ khá phức tạp. Tuy nhiên, để ý kĩ bạn sẽ thấy, thực ra bước biến đổi bao gồm 2 thao tác:
- Giảm các số có giá trị từ 2 đến \(K\) đi 1.
- Gán số đang có giá trị 1 thành \(K\).
Fun fact: Khi viết đề, mình đã cố giải thích bước biến đổi theo kiểu chú rùa 1 sẽ hút độ rùa của \(K-1\) chú rùa còn lại nhưng cảm thấy hơi kì kì nên thôi ¯\_(ツ)_/¯
Chưa nhìn ra sự kì diệu của bài toán? Gợi ý: pos[a[i]] = i là một dòng vô cùng quan trọng trong code của mình.
Nếu bạn vẫn chưa nghĩ ra, hãy đọc tiếp phần bên dưới. Còn nếu nghĩ ra rồi thì cứ đọc tiếp để chắc chắn thuật toán của mình đúng.
Thuật toán O(N)
Nếu gọi \(pos[i]\) là vị trí của số \(i\) trong hoán vị, thì mảng \(pos\) cũng là một hoán vị. Vậy ta thử xem thao tác trong bài toán thay đổi mảng \(pos\) như thế nào?
- Giảm các số có giá trị từ 2 đến \(K\) đi 1. Như vậy thì chính là gán \(pos[1] = pos[2], pos[2] = pos[3], …, pos[K-1] = pos[K]\).
- Gán số đang có giá trị 1 thành \(K\). Vậy là gán \(pos[K] = pos[1]\) (cũ).
Nói tóm lại, phép biến đổi này thay đổi hoán vị \(pos\) bằng cách chèn \(pos[1]\) vào bất kì vị trí \(K\) nào đó trong \(pos\). Ta muốn đưa hoán vị \(pos\) về hoán vị đơn vị (1, 2, …, \(N\)). Điều đó cũng có nghĩa là ta chỉ đụng vào mỗi phần tử trong hoán vị không quá một lần, bởi vì ta chỉ cần đặt nó vào một vị trí \(K\) hợp lí nào đấy và không còn quan tâm đến nó nữa.
Vậy những số nào không cần đặt vào chỗ khác? Giả sử ta thực hiện thao tác \(x\) lần, tức là các số \(pos[x+1..N]\) không bị thay đổi. Điều đó chứng tỏ ban đầu \(pos[x+1] < pos[x+2] < … < pos[N]\). Điều ngược lại cũng đúng: nếu \(pos[x+1] < pos[x+2] < … < pos[N]\) thì ta có thể dừng thao tác ở lần thứ \(x\) bằng cách chèn các số \(pos[1..x]\) vào các vị trí hợp lý để nhận được hoán vị đơn vị. Như vậy, thuật toán của bài này thực ra rất đơn giản, tìm vị trí \(x\) nhỏ nhất sao cho \(pos[x+1] < pos[x+2] < … < pos[N]\) rồi in ra \(x\).
Thống kê
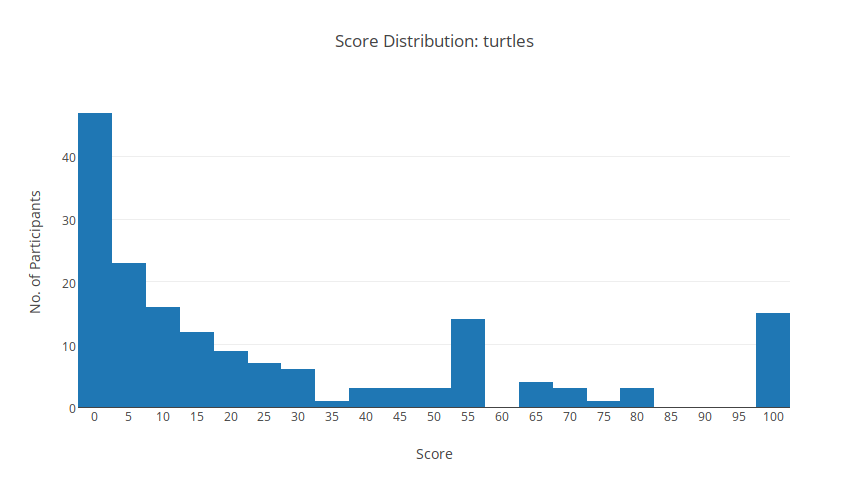
In ra \(a[1] - 1\) được 45 điểm???
Trong lúc sinh test, mình gặp phải vấn đề sau: nếu sinh test random thì khả năng số \(N-1\) đứng sau số \(N\) (\(pos[N-1] > pos[N]\)) là rất lớn, vì vậy sẽ có chừng 50% số test đáp án là \(N-1\). Mặt khác, để đáp án là \(K\) thì \(pos[K+1] < pos[K+2] < … < pos[N]\), do đó sinh random thì khả năng có đáp án bé gần như bằng không. Vậy mình đã giải quyết như nào?
Mình quyết định sinh test bằng cách: sinh trước vị trí của \(K+1, K+2, …, N\) rồi sinh random các số còn lại (tất nhiên còn thêm vài test tay nữa). Nhưng một vấn đề khác lại nảy sinh: nếu \(K\) quá nhỏ so với \(N\) (giả sử, \(K = 100\) và \(N = 500000\)), thì khả năng \(a[1] = K+1\) là vô cùng lớn (\(= 1 - K/N\)). Cách cuối cùng để giải quyết vấn đề là thêm phần truy vết các thao tác. Tuy nhiên vào phút chót, mình quyết định không làm phức tạp thêm bài toán nữa vì mình cho rằng thời gian 3.5 tiếng là khá ít, cần phải khuyến khích những người nghĩ ra đáp án hơn là đánh đố họ. Dù sao thì việc in \(a[1] - 1\) được nhiều điểm hơn cả subtask 1 cũng làm mình khá buồn :(